Известно, что х_1 и х_2 — корни уравнения х^2-9х+11=0. Не решая уравнения, найдите значение выражения: x_1^3+x_2^3.

Ответ:

\[x^{2} - 9x + 11 = 0\ \]

\[x_{1} + x_{2} = 9\]

\[x_{1} \cdot x_{2} = 11\]

\[x_{1}^{3} + x_{2}^{3} =\]

\[= \left( x_{1} + x_{2} \right)\left( x_{1}^{2} - x_{1} \cdot x_{2} + x_{2}^{2} \right) =\]

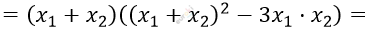
\[= 9 \cdot \left( 9^{2} - 3 \cdot 11 \right) =\]

\[= 9 \cdot (81 - 33) = 9 \cdot 48 = 432\]