Из пункта А в пункт В автомобиль ехал по шоссейной дороге длиной 21 км, а из пункта В в пункт А возвращался по грунтовой дороге длиной 20 км, затратив на обратный путь на 6 мин больше, чем на путь из пункта A в пункт В. С какой скоростью ехал автомобиль по грунтовой дороге, если по шоссе его скорость на 20 км/ч больше, чем по грунтовой дороге?

Ответ:

\[Пусть\ x\ \frac{км}{ч} - скорость\ \]

\[автомобиля\ по\ грунтовой\ \]

\[дороге;\ \]

\[(x + 20)\ \frac{км}{ч} - скорость\ \]

\[автомобиля\ по\ шоссе.\ \ \ \ \ \]

\[6\ мин = 0,1\ часа.\]

\[Составим\ уравнение:\ \]

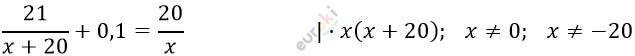
\[21x + 0,1x(x + 20) =\]

\[= 20 \cdot (x + 20)\]

\[21x + 0,1x^{2} + 2x = 20x + 400\]

\[0,1x^{2} + 23x - 20x - 400 = 0\]

\[0,1x² + 3x - 400 = 0\ \ | \cdot 10\]

\[x^{2} + 30x - 4000 = 0\]

\[x_{1} + x_{2} = - 30;\ \ \]

\[x_{1} \cdot x_{2} = - 4000;\]

\[x_{1} = 50\ \left( \frac{км}{ч} \right) - скорость\ \]

\[автомобиля\ по\ грунтовой\ \]

\[дороге.\]

\[x_{2} = - 80\ (не\ подходит).\]

\[Ответ:50\ \frac{км}{ч}.\]