Два рабочих вместе могут выполнить заказ за 12 дней. Они проработали вместе 10 дней, а затем один из рабочих в одиночку закончил выполнение заказа за 5 дней. За сколько дней каждый рабочий может выполнить данный заказ?

Ответ:

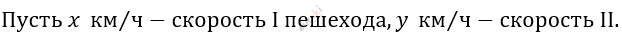
\[Встретились\ они\ \]

\[на\ середине\ пути:\]

\[6\ :2 = 3\ км.\]

\[15\ минут = \frac{1}{4}\ ч;\ \ \ \ \ \ \]

\[36\ мин = \frac{3}{5}\ ч.\]

\[Составим\ систему\ уравнений:\ \]

\[\left\{ \begin{matrix} \frac{3}{x} - \frac{3}{y} = \frac{1}{4}\text{\ \ \ \ \ \ \ \ \ } \\ (x + y) \cdot \frac{3}{5} = 6 \\ \end{matrix}\text{\ \ \ \ \ \ } \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} 12y - 12x - xy = 0 \\ x + y = 10\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix}\text{\ \ \ \ \ \ \ } \right.\ \]

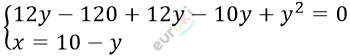
\[y^{2} + 14y - 120 = 0\]

\[y_{1} + y_{2} = - 14;\ \ \ \ \ \ \ \ \ \ \ \ \]

\[y_{1} = - 20 - не\ удовлетворяет.\]

\[y_{1} \cdot y_{2} = - 120;\ \ \ \ \ \ \ \ \ \ \ y_{2} = 6.\]

\[6\ \frac{км}{ч - скорость\ \text{II}\ пешехода}.\]

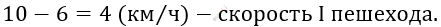
\[Ответ:6\ \frac{км}{ч;\ \ 4\ \ \frac{км}{ч.}}\]