Докажите тождество: (x+5+25/(x+5))*(x-5)/x^2=1 при каких значениях x определены обе части данного тождества?

\[\left( x + 5 + \frac{25}{x + 5} \right) \cdot \frac{x - 5}{x^{2}} =\]

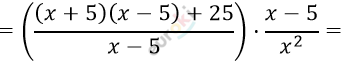
\[= \frac{\left( x^{2} - 25 + 25 \right)}{x - 5} \cdot \frac{x - 5}{x^{2}} =\]

\[= \frac{x^{2}(x - 5)}{(x - 5) \cdot x^{2}} = 1 \Longrightarrow ч.т.д.\ \ \]

\[x \neq 5;0.\]