Докажите тождество: (a+4)/(a^2-6a+9)∶(a^2-16)/(2a-6)-2/(a-4)=2/(3-a).

\[\frac{a + 4}{a^{2} - 6a + 9}\ :\frac{a^{2} - 16}{2a - 6} - \frac{2}{a - 4} =\]

\[= \frac{2}{3 - a}\]

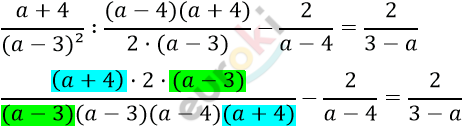
\[\frac{2}{(a - 3)(a - 4)} - \frac{2^{\backslash a - 3}}{a - 4} = \frac{2}{3 - a}\]

\[\frac{2 - 2 \cdot (a - 3)}{(a - 3)(a - 4)} = \frac{2}{3 - a}\]

\[\frac{2 - 2a + 6}{(a - 3)(a - 4)} = \frac{2}{3 - a}\]

\[\frac{8 - 2a}{(a - 3)(a - 4)} = \frac{2}{3 - a}\]

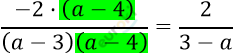
\[\frac{2}{3 - a} = \frac{2}{3 - a}.\]