Докажите равенство 1/(2sin50°)+2sin10°=1.

\[\frac{1}{2\sin{50{^\circ}}} + 2\sin{10{^\circ}} = 1\]

\[\frac{1 + 2 \cdot \left( \sin{50{^\circ}} \cdot \sin{10{^\circ}} \right)}{2\sin{50{^\circ}}} = 1\]

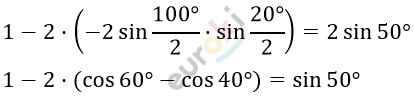
\[1 - 2 \cdot \left( \frac{1}{2} - \cos{40{^\circ}} \right) = 2\sin{50{^\circ}}\]

\[1 - 1 + 2\cos{40{^\circ}} - 2\sin{50{^\circ}} = 0\]

\[2 \cdot \left( \cos{40{^\circ}} - \sin{50{^\circ}} \right) = 0\]

\[\cos\left( \frac{\pi}{2} - 50{^\circ} \right) - \sin{50{^\circ}} = 0\]

\[\sin{50{^\circ}} - \sin{50{^\circ}} = 0\]

\[0 = 0\]