Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаДокажите, что система уравнений y=x-1; x^2+y^2-4x-2y=-1 не имеет решений.
Ответ:
\[\left\{ \begin{matrix}
y = x - 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\
x^{2} + y^{2} - 4x - 2y = - 1 \\
\end{matrix} \right.\ \]
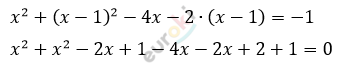
\[2x^{2} - 8x + 4 = 0\ \ \ \ \ \ \ \ \ |\ :2\]
\[x^{2} - 4x + 2 = 0\]
\[D = ( - 4)^{2} - 4 \cdot 1 \cdot 2 = 16 - 8 =\]
\[= 8\]
\[x_{1} = \frac{4 + \sqrt{8}}{2} = \frac{4 + 2\sqrt{2}}{2} =\]
\[= 2 + \sqrt{2}\]
\[x_{2} = \frac{4 - \sqrt{8}}{2} = \frac{4 - 2\sqrt{2}}{2} =\]
\[= 2 - \sqrt{2}\]
\[x_{1} = 2 + \sqrt{2}\ \ \Longrightarrow \ \ y_{1} =\]
\[= 2 + \sqrt{2} - 1 = 1 + \sqrt{2}.\]
\[x_{2} = 2 - \sqrt{2} \Longrightarrow \ \ \ \ y_{2} =\]
\[= 2 - \sqrt{2} - 1 = 1 - \sqrt{2}.\]
\[Ответ:\ \ решение\ есть:\]
\[\left( 2 + \sqrt{2};\ \ 1 + \sqrt{2} \right),\ \ \]
\[\ \left( 2 - \sqrt{2};\ \ 1 - \sqrt{2} \right).\]
