Докажите, что функция y=5x^2+7 возрастает на промежутке [0;+∞).

\[y = 5x² + 7\]

\[0 \leq x_{1} < x_{2}\]

\[y_{1} - y_{2} =\]

\[= \left( 5x_{1}^{2} + 7 \right) - \left( 5x_{2}^{2} + 7 \right) =\]

\[= 5x_{1}^{2} + 7 - 5x_{2}^{2} - 7 =\]

\[= 5 \bullet \left( x_{1}^{2} - x_{2}^{2} \right) =\]

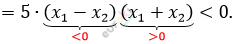
\[y_{1} - y_{2} < 0 \Longrightarrow y_{1} < y_{2} \Longrightarrow y =\]

\[= 5x^{2} + 7\ возрастает\ на\ \]

\[\lbrack 0; + \infty).\]