Докажите, что функция: f(x)=x^2-2x возрастает на промежутке [1; +∞).

Ответ:

\[f(x) = x^{2} - 2x \Longrightarrow \ возрастает\ \]

\[на\ \lbrack 1;\ + \infty)\]

\[Пусть\ \ 1 < x_{1} < x_{2}\ ,\ тогда\]

\[\text{\ \ }x_{1}^{2} - 2x_{1} - x_{2}^{2} + 2x_{2} =\]

\[= x_{1}^{2} - x_{2}^{2} - 2 \cdot \left( x_{1} - x_{2} \right) =\]

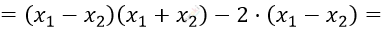
\[= \left( x_{1} - x_{2} \right)\left( x_{1} + x_{2} - 2 \right) < 0\]

\[при\ \ x_{1} < x_{2},\ \ \ \ f\left( x_{1} \right) < f\left( x_{2} \right) \Longrightarrow\]

\[\Longrightarrow функция\ \ возрастает.\ \]