Для каждого значения а решите уравнение: (x^2-(a-1)x+a-2)/(x-1)=0.

Ответ:

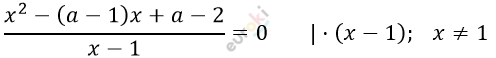
\[x^{2} - (a - 1)x + a - 2 = 0\]

\[D = (a - 1)^{2} - 4 \cdot 1 \cdot (a - 2) =\]

\[= a^{2} - 2a + 1 - 4a + 8 =\]

\[= a^{2} - 6a + 9 = (a - 3)^{2}\]

\[1)\ D = 0;\ a = 3:\]

\[x = \frac{3 - 1 \pm |3 - 3|}{2} = \frac{2}{2} = 1 \Longrightarrow\]

\[\Longrightarrow не\ подходит.\]

\[2)\ D > 0;a > 3:\]

\[x_{1} = \frac{a - 1 + a - 3}{2} = \frac{2a - 4}{2} =\]

\[= a - 2;\]

\[x_{2} = \frac{a - 1 - a + 3}{2} = \frac{2}{2} =\]

\[= 1\ (не\ подходит)\]

\[Ответ:\ \ a = 3 \Longrightarrow нет\ решения;\ \ \]

\[\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ a > 3 \Longrightarrow x = a - 2;\]

\[x \neq 1.\]