Для каждого значения а решите уравнение: 2(a-1)x^2+(a+1)x+1=0.

Ответ:

\[2 \cdot (a - 1)x² + (a + 1)x + 1 = 0\]

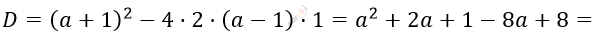
\[= a^{2} - 6a + 9 = (a - 3)^{2}\]

\[1)\ \ При\ D = 0:\]

\[(a - 3)^{2} = 0\]

\[\ a - 3 = 0\]

\[a = 3.\]

\[x = \frac{- (a + 1)}{2 \cdot 2 \cdot (a - 1)} = \frac{- a - 1}{4a - 4} =\]

\[= \frac{- 3 - 1}{4 \cdot 3 - 4} = \frac{- 4}{12 - 4} = - \frac{4}{8} =\]

\[= - 0,5.\]

\[2)\ При\ D > 0;\ a \neq 3:\]

\[x_{1,2} = \frac{- (a + 1) \pm \sqrt{(a - 3)^{2}}}{2 \cdot 2 \cdot (a - 1)} =\]

\[= \frac{- a - 1 \pm |a - 3|}{4 \cdot (a - 1)};\]

\[x_{1} = \frac{- a - 1 + a - 3}{4 \cdot (a - 1)} =\]

\[= \frac{- 4}{4 \cdot (a - 1)} = - \frac{1}{a - 1};\]

\[x_{2} = \frac{- a - 1 - a + 3}{4 \cdot (a - 1)} =\]

\[= \frac{- 2a + 2}{4 \cdot (a - 1)} = \frac{1 - a}{2 \cdot (a - 1)} =\]

\[= - \frac{(a - 1)}{2 \cdot (a - 1)} = - 0,5.\]

\[Ответ:если\ a = 3;то\ x = - 0,5;\ \]

\[\ \ \ \ \ \ \ \ \ \ \ \ \ \ если\ a \neq 3;\ a \neq 1;\ \]

\[то\ x_{1} = - \frac{1}{a - 1}\ или\ x_{2} = - 0,5;\ \]

\[\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ если\ a = 1;то\ x = - 0,5.\]