Для каждого значения a решите неравенство: x^2+(1-3a)x+2a^2-3a-2>0.

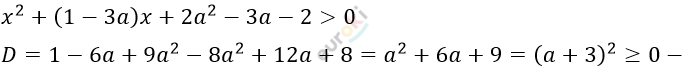
\[при\ любом\ значении\ a.\]

\[x_{1} = \frac{- (1 - 3a) - (a + 3)}{2} =\]

\[= \frac{- 1 + 3a - a - 3}{2} = \frac{2a - 4}{2} =\]

\[= a - 2;\]

\[x_{2} = \frac{- (1 - 3a) + (a + 3)}{2} =\]

\[= \frac{- 1 + 3a + a + 3}{2} = \frac{4a + 2}{2} =\]

\[= 2a + 1.\]

\[\left( x - x_{1} \right)\left( x - x_{2} \right) > 0\]

\[x < x_{1};\ \ \ x > x_{2}.\]

\[a - 2 > 1 + 2a\]

\[a < - 3.\]

\[Если\ a < - 3:\]

\[x \in ( - \infty;1 + 2a) \cup (a - 2;\ + \infty).\]

\[Если\ a = - 3:\]

\[x \in ( - \infty; - 5) \cup ( - 1; + \infty).\]

\[Если\ a > - 3:\]

\[x( - \infty;a - 2) \cup (1 + 2a; + \infty).\]