Диагональ прямоугольника равна 13 см, а его периметр равен 34 см. Найдите стороны прямоугольника.

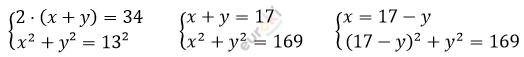
\[289 - 34y + y^{2} + y^{2} - 169 = 0\]

\[2y^{2} - 34y + 120 = 0\ \ \ \ \ |\ :2\]

\[y^{2} - 17y + 60 = 0\]

\[D = ( - 17)^{2} - 4 \cdot 1 \cdot 60 =\]

\[= 189 - 240 = 49;\ \ \ \ \ \sqrt{D} = 7.\]

\[y_{1} = \frac{17 + 7}{2} = \frac{24}{2} = 12;\ \ \ \ \ \]

\[\text{\ \ }y_{2} = \frac{17 - 7}{2} = \frac{10}{2} = 5\]

\[x_{1} = 17 - 12 = 5;\ \ \ \ \ \ \ \ \ \ \ \ \]

\[\text{\ \ \ \ \ }x_{2} = 17 - 5 = 12\]

\[Ответ:5\ см\ и\ 12\ см.\]