Дано: a<0 и b>0. Сравните: 1/(a-5b) и 1/b.

Ответ:

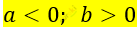
\[\frac{1}{a - 5b} < \frac{1}{b};\ \ \ \ так\ как\ \ \]

\[\frac{1^{\backslash b}}{a - 5b} - \frac{1^{\backslash a - 5b}}{b} = \frac{b - a + 5b}{b(a - 5b)} =\]

\[= \frac{6b - a}{b(a - 5b)}\]

\[Так\ как\ (6b - a) > 0;\ \ b > 0;\ \ \]

\[a - 5b < 0;то\]

\[\frac{6b - a}{b(a - 5b)} < 0.\ \]

\[Получаем:\]

\[\frac{1}{a - 5b} < \frac{1}{b}.\]