Автомобиль проехал первую часть пути за 2,6 ч со скоростью 78 км/ч, а вторую часть — за 3,9 ч. С какой скоростью автомобиль проехал вторую часть пути, если средняя скорость в течение всего времени движения составляла 70,2 км/ч.

\[t_{1} = 2,6\ ч;\ \ t_{2} = 3,9\ ч;\]

\[V_{1} = 78\ \frac{км}{ч};\ \]

\(\ V_{ср.} = 70,2\ \frac{км}{ч}\text{.\ \ }\)

\[t_{об.} = t_{1} + t_{2} = 2,6 + 3,9 = 6,5\ ч.\]

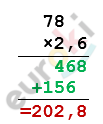
\[S_{1} = V_{1} \cdot t_{1} = 2,6 \cdot 78 =\]

\[= 202,8\ (км).\]

\[Пусть\ x\ \frac{км}{ч} - это\ V_{2},\ тогда\ \]

\[S_{2} = V_{2} \cdot t_{2} = 3,9x\ км.\]

\[S_{об.} = 202,8 + 3,9x\ (км);\]

\[V_{ср.} = (202,8 + 3,9x)\ :6,5 =\]

\[= 70,2\ \ | \cdot 2\]

\[202,8 + 3,9x = 456,3\]

\[3,9x = 456,3 - 202,8\]

\[3,9x = 253,5\]

\[x = 2535\ :39\]

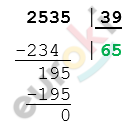
\[x = 65\ \frac{км}{ч} - скорость\ V_{2}.\]

\[Ответ:65\ \frac{км}{ч}.\]