Свободное падение тел. Движение тела, брошенного вертикально вверх/вниз | Конспект

Свободное падение – это движение тела только под действием силы тяжести.

Ускорение свободного падения – показывает, как меняется скорость тела при свободном падении.

g \(\approx\) 9,8 (\(\approx\) 10) м/с² – ускорение свободного падения

Свободное падение

V₀ = 0

V_y = gt – скорость при свободном падении

h = \(\frac{gt^{2}}{2}\) – высота

Движение тела вертикально вниз

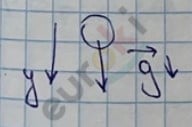
V_y = V_0y + gt – скорость

h = V_0yt + \(\frac{gt^{2}}{2}\) – высота

Движение тела вертикально вверх

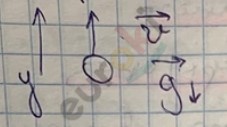
V_y = V_0y – gt

h = V_0yt – \(\frac{gt^{2}}{2}\)

На максимальной высоте V_y = 0

0 = V_0y – gt => t = \(\frac{V_{0y}}{g}\)

V_0y = gt

h_max = \(\frac{gt^{2}}{2}\) – максимальная высота подъёма

t = \(\sqrt{\frac{{2h}_{\max}}{g}}\)

Сила тяжести – сила, с которой земля притягивает к себе другие тела.

F_max = mg – сила тяжести

[F] = Н

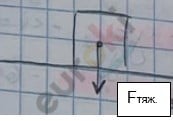
Вес тела – сила, с которой тело давит на опору или растягивает подвес вследствие притяжения к земле.

Если тело движется равномерно или покоится, то вес тела равен силе тяжести.

Если V = const, то P = mg – вес тела.

[P] = Н

Тело двигается вертикально вверх:

P = m (g + a)

P > F_тяж.

Тело движется вертикально вниз:

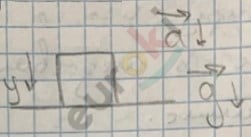
P = m (g – a)

P < F_тяж.

Если a = g, то Р = 0

Закон всемирного тяготения

Два тела притягиваются друг к другу с силой, прямо пропорциональной массе каждого из них и обратно пропорциональной квадрату расстояния между ними.

F = G \(\frac{m_{1}m_{2}}{r^{2}}\) – закон всемирного тяготения

m₁m₂ – масса тел, кг

r – расстояние между телами, м

F – сила, Н

G = 6,67 • 10^-11 \(\frac{Н\ м^{2}}{{кг}^{2}}\) – гравитационная постоянная

Физический смысл гравитационной постоянной – она показывает, с какой силой притягиваются друг к другу тела массой 1 кг при расстоянии между ними 1 м.

Условия, определяющие границы применимости закона всемирного тяготения

1. Если размеры тел пренебрежимо малы по сравнению с расстоянием между ними.

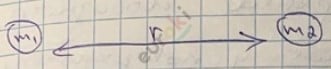
2. Если оба тела однородны и имеют шарообразную форму.

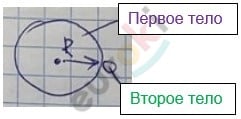
3. Если одно из взаимодействующих тел – шар, размеры и масса которого значительно больше, чем у второго тела, находящегося на поверхности этого шара или вблизи неё.

Учитывая, что F = mg (по II закону), mg = G \(\frac{\text{mM}}{R^{2}}\)

g = \(\frac{\text{GM}}{R^{2}}\) – ускорение свободного падения у поверхности планеты

g = \(\frac{\text{GM}}{{(R + h)}^{2}}\) – ускорение свободного падения на высоте h над поверхностью планеты

M – масса планеты, кг

R – радиус планеты, м

h – высота над поверхностью планеты, м