Смешанное соединение потребителей. Метод эквивалентного сопротивления | Конспект

Во многих цепях встречаются участки с последовательным и параллельным соединением. Такое соединение называется смешанным.

Для поиска общего сопротивления используют метод эквивалентного сопротивления: находят участок с одним типом соединения, рассчитывают его сопротивление, потом заменяют этот участок одним потребителем, таким образом упрощают цепь.

Рассмотрим на конкретном примере:

Даны 4 резистора с сопротивлением 2 Ом каждый.

Построить всевозможные схемы их соединения и рассчитать для каждой общее сопротивление.

R_общ. = R₁ + R₂ + R₃ + R₄ = 80 Ом

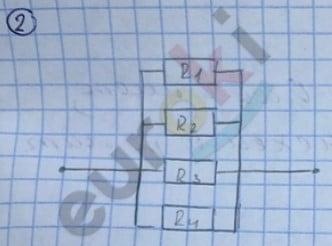
\(\frac{1}{R_{общ}}\) = \(\frac{1}{R_{1}}\) + \(\frac{1}{R_{2}}\) + \(\frac{1}{R_{3}}\) + \(\frac{1}{R_{4}}\) = 2 Ом

R_общ. = \(\frac{1}{2}\) Ом

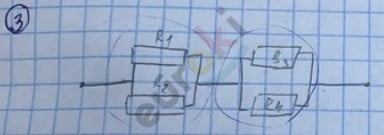
\(\frac{1}{R_{1,2}}\) = \(\frac{1}{R_{1}}\) + \(\frac{1}{R_{2}}\) = 1 Ом

\(\frac{1}{R_{3,4}}\) = 1 Ом

\(\frac{1}{R_{общ}}\) = 1 Ом

\(\frac{1}{R_{общ}}\) = \(\frac{1}{R_{1,2}}\) + \(\frac{1}{R_{3,\ 4}}\) = 2 Ом

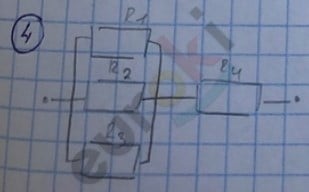
\(\frac{1}{R_{общ}}\) = \(\frac{1}{R_{1,2,3}}\) + \(\frac{1}{R_{1}}\) + \(\frac{1}{R_{2}}\ \)+ \(\frac{1}{R_{3}}\)

\(\frac{1}{R_{1,2,3}}\) = \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) = \(\frac{3}{2}\)

\(\frac{1}{R_{общ}}\) = \(\frac{2}{3}\) Ом