Скорость прямолинейного равноускоренного движения. График скорости | Конспект

Мгновенная скорость – скорость в данный момент времени.

Равноускоренное движение – вид движения, при котором тело за равные промежутки времени изменяет скорость на одно и то же число.

Ускорение – векторная величина, которая характеризуется не только модулем, но и направлением.

\(\overrightarrow{a}\) = \(\frac{\overrightarrow{V} - \ \overrightarrow{V_{0}}}{t}\) – ускорение

V₀ – начальная скорость, м/с

V – конечная скорость, м/с

t – время, с

[а] = \(\frac{\frac{м}{с}}{с}\) = \(\frac{м}{с^{2}}\)

a_x = \(\frac{V_{x} - \ V_{0x}}{t}\)

a = \(\frac{\mathrm{\Delta}V}{\mathrm{\Delta}t}\)

\(\mathrm{\Delta}\)V – изменение скорости, м/с

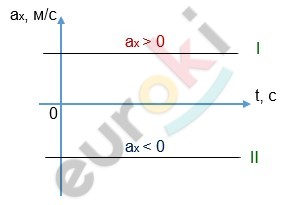
I – равноускоренное движение

II – равнозамедленное движение

\(\overrightarrow{a}\)t = \(\overrightarrow{V}\) – \(\overrightarrow{V}\)₀

\(\overrightarrow{V}\) = \(\overrightarrow{V}\)₀ + \(\overrightarrow{a}\)t – скорость при равноускоренном движении

V_x = V_0x + a_xt

V_y = V_0y + a_yt

Если V₀ = 0, то V = at

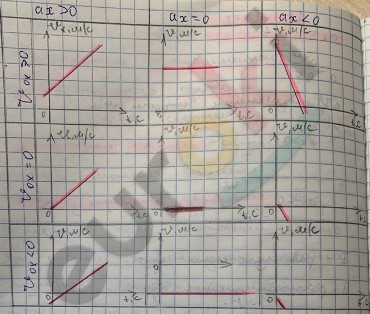
Перемещение тела при прямолинейном равноускоренном движении

S = V_0xt + \(\frac{a_{x}t^{2}}{2}\)

S_x = V_0xt + \(\frac{a_{x}t^{2}}{2}\)

Проекция векторных величин на ось Х:

\(v_{х}\) = \(v_{0х}\) + \(a_{x}\) · t

\(v_{х}\) = \(a_{x}\) · t

Зависимость проекции вектора скорости от времени при равноускоренном движении линейная, значит, графиком функции \(v_{х}\)(t) будет прямая.