Равноускоренное движения (РУД). Ускорение | Конспект

Равноускоренным движением называется такое движение, при котором за любые равные промежутки времени скорость тела изменяется на одинаковую векторную величину.

а) Случай ускорения тела

За \(\mathrm{\Delta}\)t скорость изменяется на \(\mathrm{\Delta}\overrightarrow{v}\)→:

За 2\(\mathrm{\Delta}\)t скорость изменяется на 2\(\mathrm{\Delta}\overrightarrow{v}\):

За 3\(\mathrm{\Delta}\)t:

б) Случай торможения тела

За \(\mathrm{\Delta}\)t скорость изменяется на \(\mathrm{\Delta}\overrightarrow{v}\)←:

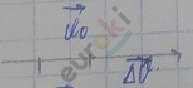
За 2\(\mathrm{\Delta}\)t:

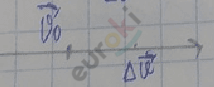
За 3\(\mathrm{\Delta}\)t:

Точка остановки тела

За 4\(\mathrm{\Delta}\)t:

Движение в обратную сторону

в) Случай бросания камня горизонтально

За \(\mathrm{\Delta}\)t скорость изменяется на \(\mathrm{\Delta}\overrightarrow{v}\)↓

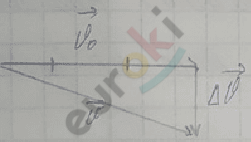
За 2\(\mathrm{\Delta}\)t:

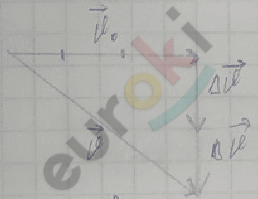
За 3\(\mathrm{\Delta}\)t:

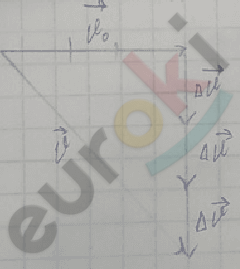
Во всех трёх случаях общая скорость \(\overrightarrow{v}\) = \({\overrightarrow{v}}_{0}\) + n · \(\mathrm{\Delta}\overrightarrow{v}\).

n – количество промежутков времени

n = \(\frac{t}{\mathrm{\Delta}t}\)

\(\overrightarrow{v}\) = \({\overrightarrow{v}}_{0}\) + \(\frac{t}{\mathrm{\Delta}t}\) · \(\mathrm{\Delta}\overrightarrow{v}\)

\(\overrightarrow{v}\) = \({\overrightarrow{v}}_{0}\) + t · \(\frac{\mathrm{\Delta}\overrightarrow{v}}{\mathrm{\Delta}t}\)

При равноускоренном движении \(\frac{\mathrm{\Delta}\overrightarrow{v}}{\mathrm{\Delta}t}\) – const

\(\overrightarrow{a}\) = \(\frac{\mathrm{\Delta}\overrightarrow{v}}{\mathrm{\Delta}t}\) – ускорение (изменение скорости)

Ускорением тела при равноускоренном движении называется физическая величина, равная отношению изменения скорости тела ко времени, за которое оно произошло.

[а] = \(\frac{м}{с^{2}}\)

\(\mathrm{\Delta}\overrightarrow{v}\) = \(\overrightarrow{v}\) – \({\overrightarrow{v}}_{0}\)

\(\mathrm{\Delta}\)t = t – \(t_{0}\)

Удобно брать t = 0

\(\overrightarrow{a}\) = \(\frac{\overrightarrow{v}\ –\ {\overrightarrow{v}}_{0}}{t}\)

\(\overrightarrow{v}\) = \({\overrightarrow{v}}_{0}\) + \(\overrightarrow{a}\)t

\(v_{x}\) = \(v_{0x}\) + \(a_{x}\)t

Пусть \(v_{0x}\) > 0:

\(a_{x}\) > 0 → \(v_{x}\)↑

\(a_{x}\) < 0 → \(v_{x}\)↓