Работа силы | Конспект

Второй закон Ньютона в форме \(\mathrm{\Delta}\overrightarrow{p}\) = \(\overrightarrow{F}\mathrm{\Delta}\)t позволяет определить, как меняется скорость тела \(\overrightarrow{v}\) по модулю и направлению, если на него в течение времени \(\mathrm{\Delta}\)t действует сила \(\overrightarrow{F}\).

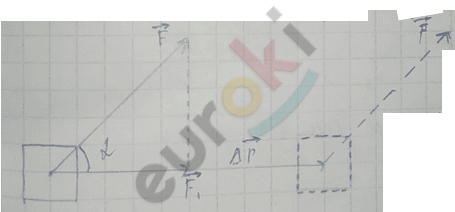
А = \(F_{r}\) |\(\mathrm{\Delta}\overrightarrow{r}\)| – справедливо только в том случае, когда сила постоянная и перемещение тела происходит вдоль прямой.

Если угол между силой и перемещением обозначить через \(\alpha\), то \(F_{r}\) = F\(\cos\alpha\), следовательно, работа равна А = F|\(\mathrm{\Delta}\overrightarrow{r}\)|\(\cos\alpha\).

Работа силы равна произведению модулей силы и перемещения точки приложения силы и косинусы угла между ними.

Если на тело действует несколько сил, то проекция результирующей силы на перемещение равна сумме проекций отдельных сил:

\(F_{r}\) = \(F_{1r}\) + \(F_{2r}\) + ...

Поэтому для работы результирующей силы получаем:

А = \(F_{1r}|\mathrm{\Delta}\overrightarrow{r}|\) + \(F_{2r}|\mathrm{\Delta}\overrightarrow{r}|\ \)+ ... = \(А_{1}\) + \(А_{2}\) + ...

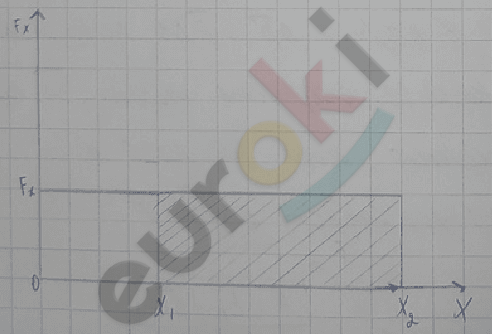
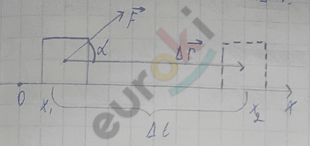
Пусть тело движется вдоль оси \(0_{х}\), тогда F\(\cos\alpha\) = \(F_{x}\), \(|\mathrm{\Delta}\overrightarrow{r}|\ \)= \(\mathrm{\Delta}\)x.

Для работы силы получаем: А = F|\(\mathrm{\Delta}\overrightarrow{r}\)|\(\cos\alpha\) = \(F_{x}\mathrm{\Delta}\)x.

1 Дж = 1 Н · 1 м = 1 Н · м

Джоуль – это работа, совершаемая силой 1 Н на перемещении 1 м, если направление силы и перемещения совпадают.

Часто используют краткую единицу работы – килоджоуль: 1 кДж = 1000 Дж.

Приведено определение работы силы \(\overrightarrow{F}\) при перемещении тела на \(|\mathrm{\Delta}\overrightarrow{r}|\), составляющим угол \(\alpha\) с направлением силы: А = \(\overrightarrow{F}\)|\(\mathrm{\Delta}\overrightarrow{r}\)|\(\cos\alpha\).