Прямолинейное движение. Равномерное движение по окружности. Центростремительное ускорение | Конспект
1. Если движение криволинейное, то скорость и ускорение лежат не на одной прямой.

2. Криволинейное движение может быть равномерно (например, движение по кругу).
\(\overrightarrow{a}\) = \(\frac{\mathrm{\Delta}\overrightarrow{v}}{\mathrm{\Delta}t}\)
\(v_{1}\) = \(v_{2}\)
\({\overrightarrow{v}}_{1}\) \(\neq\) \({\overrightarrow{v}}_{2}\)
\(\overrightarrow{a}\) = \(\frac{{\overrightarrow{v}}_{2} - \ {\overrightarrow{v}}_{1}\ }{\mathrm{\Delta}t}\) = \(\frac{\mathrm{\Delta}\overrightarrow{v}}{\mathrm{\Delta}t}\) \(\neq\) 0
\(\mathrm{\Delta}\)v = \(\frac{\mathrm{\Delta}t}{v_{2}}\) – \({\overrightarrow{v}}_{2}\)
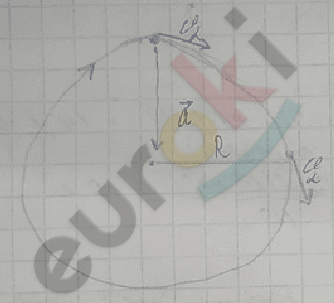
Любое криволинейное движение является движением с ускорением, так как в его ходе имеется изменение направления скорости.
\(\overrightarrow{a}\) направлено в центр
\(\overrightarrow{a}\) \(\bot\) \(\overrightarrow{v}\)
a = \(\frac{v^{2}}{R}\)
\({\overrightarrow{a}}_{ус.}\) – центростремительное ускорение (нормальное ускорение)


