Движение с постоянным ускорением свободного падения | Конспект

Свободное падение – движение без начальной скорости под действием силы тяжести (равноускоренное).

g – ускорение свободного падения

g = 9,8 \(\frac{м}{с^{2}}\) \(\approx\) 10 \(\frac{м}{с^{2}}\)

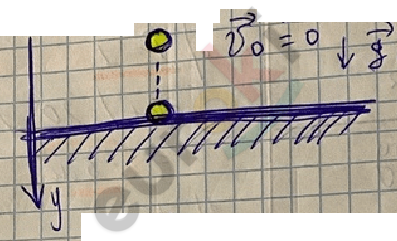
\(V_{y}\) = \(g_{y}\)t

y = \(y_{0}\) + \(\frac{g_{y}t^{2}}{2}\)

S = y – \(y_{0}\)

Движение вертикально вниз с начальной скоростью (равноускоренное)

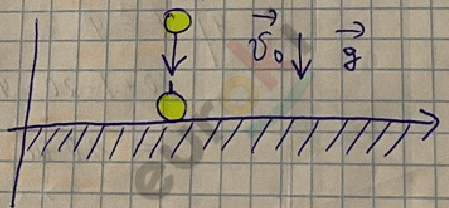
\(V_{y}\) = \(V_{0y}\) + \(g_{y}\)t

y = \(y_{0}\) + \(V_{0y}\)t + \(\frac{g_{y}t^{2}}{2}\)

Движение вертикально вверх с начальной скоростью (равнозамедленное)

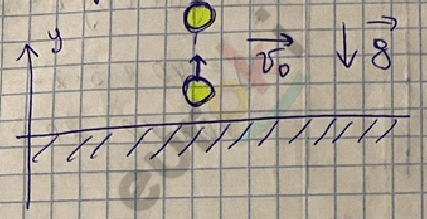
\(V_{y}\) = \(V_{0y}\) – \(g_{y}\)t

y = \(y_{0}\) + \(V_{0y}\)t – \(\frac{g_{y}t}{2}\)

Движение тела под углом к горизонту

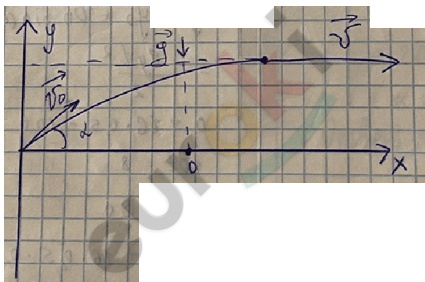
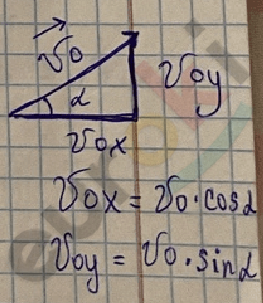
\(0_{х}\) : \(V_{х}\) = \(V_{0}\) · \(\cos\alpha\)

\(g_{х}\) = 0 |\(\overrightarrow{g}\bot 0_{х}\)|

х = \(х_{0}\) + \(V_{0}\) · \(\cos\alpha\)

\(g_{х}\) = 0

\(0_{y}\) : \(V_{y}\) = 0

\(0\) = \(V_{0}\) · \(\sin{\alpha\ }\)– \(g_{y}\)t

y = \(y_{0}\) + \(V_{0}\) · \(\sin{\alpha\ }\)· t – \(\frac{g_{y}t^{2}}{2}\)