Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 9 класс Атанасян ФГОС Задание 859
Задание 859
\[\boxed{\mathbf{859.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[ABCD - выпуклый\ \]
\[четырехугольник;\]
\[M;N;P;Q - середины\ сторон;\]
\[MP + NQ = \frac{AB + BC + CD + AD}{2}.\]
\[\mathbf{Доказать:}\]
\[ABCD - параллелограмм.\]
\[\mathbf{Доказательство.}\]
\[1)\ Пусть\ стороны\ ABCD\ \]
\[попарно\ не\ параллельны\ \]
\[(см.\ №858):\]
\[MP < \frac{AD + BC}{2};\text{\ \ }\]
\[NQ < \frac{AB + CD}{2}.\]
\[Значит:\]
\[MP + NQ \leq \frac{AB + BC + CD + AD}{2}.\]
\[Что\ противоречит\ условию.\]
\[2)\ Допустим,\ что\ AD \nparallel BC,\ \]
\[но\ AB \parallel CD:\ \]
\[MP \leq \frac{AD + BC}{2};\text{\ \ }\]
\[NQ = \frac{AB + CD}{2};\]
\[MP + NQ \leq\]
\[\leq \frac{AB + BC + CD + AD}{2}.\]
\[Равенство\ выполняется,\ но\ \]
\[только\ иногда.\]
\[3)\ При\ AD \parallel BC\ и\ AB \parallel CD:\]
\[MP = \frac{AD + BC}{2};\text{\ \ }\]
\[NQ = \frac{AB + CD}{2};\]
\[MP + NQ = \frac{AB + BC + CD + AD}{2}.\]
\[Равенство\ всегда\ выполняется,\ \]
\[если\ стороны\ попарно\ \]
\[параллельны:\]
\[ABCD - параллеграмм.\]
\[\mathbf{Что\ и\ требовалось\ доказать.}\]
\[\boxed{\mathbf{859.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
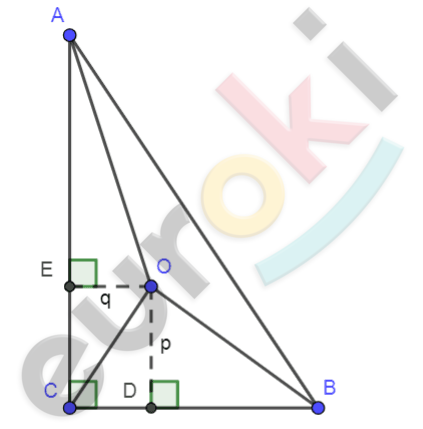
\[\mathrm{\Delta}ABC;\ \]
\[\angle C = 90{^\circ};\]
\[S_{\text{OAB}} = S_{\text{OAC}} = S_{\text{OBC}}.\]
\[\mathbf{Доказать:}\]
\[OA² + OB² = 5OC².\]
\[\mathbf{Доказательство.}\]
\[1)\ Проведем\ перпендикуляры\ \]
\[из\ точки\ O\ на\ катеты.\ \]
\[2)\ Допустим:\]
\[OD = p;\ \ OE = q;\ \ AB = c;\ \ \]
\[AC = b;\ \ BC = a;\ \frac{1}{2}ab = S.\]
\[Получим:\]
\[S_{\text{AOB}} = S_{\text{OAC}} = S_{\text{OBC}} = \frac{S}{3}.\]
\[3)\ Запишем\ равенства:\]
1.
\(S_{\text{OAC}} = S_{\text{OBC}};\ \)
\[\frac{1}{2}bq = \frac{1}{2}ap = \frac{S}{3};\ \ \ \ \]
\[q = \frac{a}{3};\ \ \]
\[p = \frac{b}{3}.\]
\[2.\ \ \ \]
\[CD = q = \frac{a}{3};\ \ \ \ \ \]
\[BD = a - q = \frac{2q}{3};\ \ \]
\[EC = p = \frac{b}{3};\ \ \ \ \]
\[\ AE = b - p = \frac{2b}{3}.\]
\[3.\ \ \ p^{2} = OB^{2} - BD^{2} =\]
\[= OC^{2} - CD^{2};\ \ \]
\[\frac{b^{2}}{9} = OB^{2} - \frac{4a^{2}}{9} = OC^{2} - \frac{a^{2}}{9}.\]
\[4.\ \ \ \]
\[q^{2} = OC^{2} - CE^{2} = OA^{2} - AE^{2};\ \ \]
\[\frac{a^{2}}{9} = OC^{2} - \frac{b^{2}}{9} = OA^{2} - \frac{4b^{2}}{9}.\]
\[4)\ Получим:\]
\[OA^{2} = \frac{a^{2} + 4b^{2}}{9};\ \ \ \]
\[OB^{2} = \frac{4a^{2} + b^{2}}{9};\ \ \]
\[OC^{2} = \frac{a^{2} + b^{2}}{9}.\]
\[Откуда:\]
\[OA^{2} + OB^{2} =\]
\[= \frac{a^{2} + 4b^{2}}{9} + \frac{4a^{2} + b^{2}}{9} =\]
\[= \frac{5a^{2} + 5b^{2}}{9} = 5 \bullet \left( \frac{a^{2} + b^{2}}{9} \right) =\]
\[= 5OC^{2}.\]
\[\mathbf{Что\ и\ требовалось\ доказать.}\]
