Алгебра
Английский
Биология
География
Геометрия
Русский
История
Обществознание
Физика
Химия
Информатика
Литература
МатематикаГДЗ по алгебре и начала математического анализа 11 класс Колягин Задание 959
Задание 959
\[1)\ \left\{ \begin{matrix} \log_{y}x + \log_{x}y = \frac{5}{2} \\ x + y = a + a^{2}\text{\ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \]
\[\log_{y}x + \log_{x}y = \frac{5}{2}\]
\[\log_{y}x - \frac{5}{2} + \frac{1}{\log_{y}x} = 0\]
\[2\log_{y}^{2}x - 5\log_{y}x + 2 = 0\]
\[D = 25 - 16 = 9\]
\[\log_{y}x_{1} = \frac{5 - 3}{2 \bullet 2} = \frac{1}{2};\]
\[\log_{y}x_{2} = \frac{5 + 3}{2 \bullet 2} = 2;\]
\[x = y^{\frac{1}{2}} = \sqrt{y}\ ;\ \ x = y^{2}.\]
\[1)\ \sqrt{y} + y = a + a^{2}\]
\[y + \sqrt{y} - \left( a^{2} + a \right) = 0\]
\[D = 1^{2} + 4\left( a^{2} + a \right) =\]
\[= 4a^{2} + 4a + 1 = (2a + 1)^{2}\]
\[\sqrt{y_{1}} = \frac{- 1 - (2a + 1)}{2} = - a - 1;\]
\[\sqrt{y_{2}} = \frac{- 1 + (2a + 1)}{2} = a;\]
\[y_{1} = ( - a - 1)^{2} = (a + 1)^{2};\]
\[y_{2} = a^{2}.\]
\[x_{1} = - a - 1;\ x_{2} = a.\]
\[2)\ y^{2} + y = a + a^{2}\]
\[y^{2} + y - \left( a^{2} + a \right) = 0\]
\[D = 1^{2} + 4\left( a^{2} + a \right) =\]
\[= 4a^{2} + 4a + 1 = (2a + 1)^{2}\]
\[y_{1} = \frac{- 1 - (2a + 1)}{2} = - a - 1;\]
\[y_{2} = \frac{- 1 + (2a + 1)}{2} = a;\]
\[x_{1} = ( - a - 1)^{2} = (a + 1)^{2};\]
\[x_{2} = a^{2}.\]
\[Для\ первой\ пары\ корней:\]
\[a > 0;\ a^{2} > 0;\ a \neq 1;\ a^{2} \neq 1;\]
\[a > 0;\ a \in R;\ a \neq 1;\ a \neq \pm 1;\]
\[a > 0;\ \ \ a \neq 1.\]
\[Для\ второй\ пары\ корней:\]
\[- a - 1 > 0;(a + 1)^{2} > 0;\ \ \ \]
\[- a - 1 \neq 1;\ \ \ (a + 1)^{2} \neq 1;\]
\[a < - 1;\ \ \ a \in R;\ \ \ \]
\[a \neq - 2;\ \ \ (a + 1)^{2} \neq 1;\]
\[a < - 1;\ \ \ a \neq - 2;\]
\[Ответ:\ \ \]
\[\left( a;\ a^{2} \right);\ \left( a^{2};\ a \right)\ при\ a > 0\ и\ a \neq 1;\]
\[\left( - a - 1;\ (a + 1)^{2} \right);\ \]
\[\left( (a + 1)^{2};\ - a - 1 \right)\ при\ \]
\[a < - 1\ и\ a \neq - 2.\]
\[2)\ \left\{ \begin{matrix} \left( |x| - 5 \right)^{2} + (y - 4)^{2} = 4 \\ (x - 2)^{2} + y^{2} = a^{2}\text{\ \ \ \ \ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \]
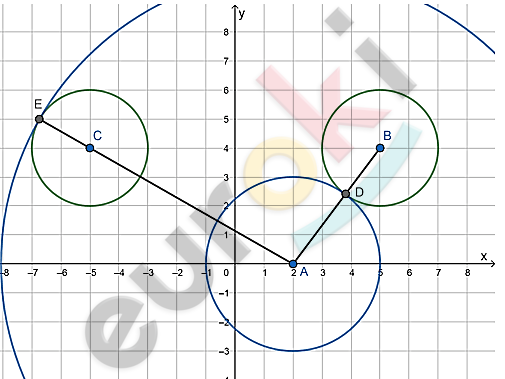
\[Первая\ точка:\]
\[a = AD = AB - BD =\]
\[= \sqrt{(5 - 2)^{2} + 4^{2}} - \sqrt{4} =\]
\[= \sqrt{9 + 16} - 2 = \sqrt{25} - 2 =\]
\[= 5 - 2 = 3.\]
\[Вторая\ точка:\]
\[a = AE = AC + EC =\]
\[= \sqrt{(2 + 5)^{2} + 4^{2}} - \sqrt{4} =\]
\[= \sqrt{49 + 16} - 2 = \sqrt{65} - 2.\]
\[Ответ:\ \ 3;\ \sqrt{65} + 2.\]
